The limitations of quantitative financial models and the risks of over-reliance on them were starkly demonstrated on a global scale by the rise and collapse of Long-Term Capital Management (LTCM). The hedge fund assembled a team that included Myron Scholes and Robert Merton. LTCM sought to exploit small inefficiencies in financial markets using sophisticated mathematical models, but its eventual failure underscored the dangers of assuming that such models could fully capture the complexities of real-world market dynamics. It received a $3.6 billion bailout from a group of 14 banks in a deal brokered by the Federal Reserve Bank of New York in 1998 [1].
LTCM Strategy: Arbitrage and Market Inefficiencies
LTCM was founded in 1994 by John Meriwether, the former head of bond trading at Salomon Brothers; Scholes and Merton were also involved from its inception. The fund aimed to exploit small inefficiencies in the pricing of securities using advanced statistical arbitrage strategies. These strategies were built on the assumption that markets are rational, inefficiencies are temporary, and asset prices would mean-revert in a predictable manner, like the way physical systems return to equilibrium in classical mechanics.
This assumption is closely linked to the idea of Brownian motion, which underlies the Black-Scholes model and other financial stochastic processes. In the same way that a particle undergoing Brownian motion oscillates around an equilibrium position due to small, random fluctuations, LTCM’s models presumed that asset prices would deviate randomly but ultimately return to their fair value.
The fund’s strategies were largely based on fixed-income arbitrage, convergence trading, and market-neutral strategies, seeking to capitalize on temporary mispricing between assets. One such example was LTCM’s bet on on-the-run vs. off-the-run Treasury Bonds, where they expected yields to converge over time. These are conceptually simple but rather difficult to implement. Its assumptions lie within the Black Scholes Framework.
A basic example of LTCM’s arbitrage strategy is illustrated below:
Assume two bonds 
and 
with initial prices 
and 
. The price of bond is exprected to rise and s a ‘long’ position is taken: it is bought at time 0 for and sold at time t for 
. The price of bond on the other hand is expected to fall, so a ‘short’ position is taken: it is sold at the price for a delivery at time t when the price will be 
. If the prices converge, i.e. if
– > –
profits are generated [2].
Mathematically, the approach relied on Gaussian statistical models, which assumed that asset prices followed a Bachelier-Wiener stochastic process and that their future volatility could be estimated from past data. LTCM’s quantitative approach assumed stationarity and ergodicity, meaning that past patterns would persist in the future and that large deviations from expected price movements were highly improbable.
This approach was leveraged across thousands of trades to generate substantial absolute gains from small pricing inefficiencies.
The Rise of LTCM: A Quantitative Powerhouse
Following its strategic approach to exploiting market inefficiencies LTCM’s early years were marked by unprecedented financial success. The fund posted exceptional annual returns that significantly outperformed market benchmarks.
- 1994: LTCM achieved a 20% return, outperforming the S&P 500’s modest gain of 1.3%.
- 1995: The fund reported an astonishing 42.8% return, compared to the S&P 500’s 37.2% increase.
- 1996: LTCM continued its dominance with a 40.8% return, while the S&P 500 rose 22.6%.
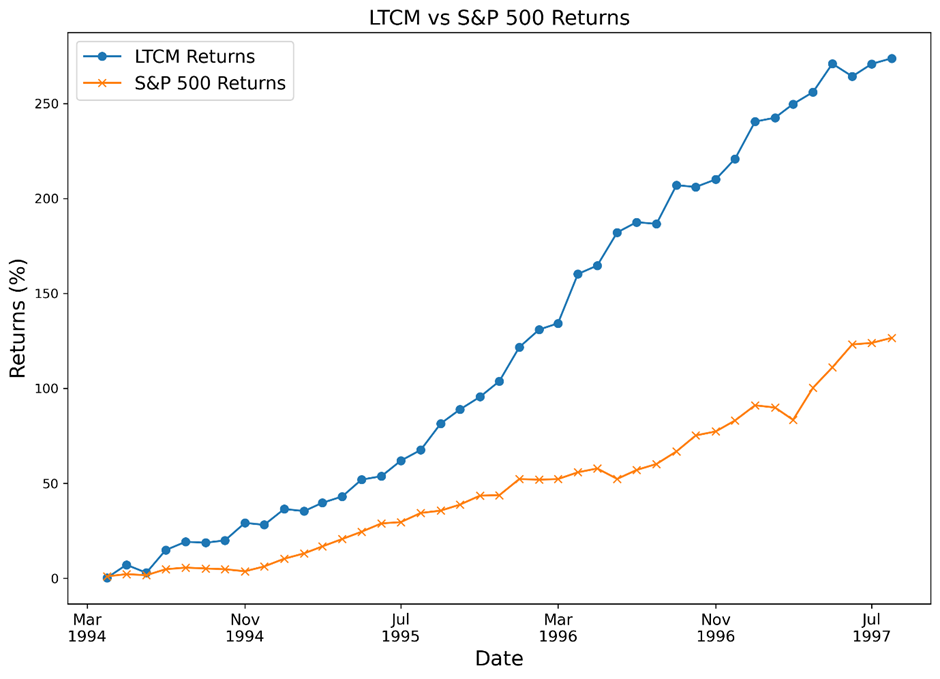
By the end of 1997, LTCM managed over $100 billion in assets, despite only having $4.72 billion in firm capital. Investors, including central banks, pension funds, and major financial institutions, eagerly poured money into the firm, viewing it as a quantitative powerhouse capable of producing consistent, low-risk profits.
A large reason for LTCM’s remarkable success was its extreme use of leverage. The firm’s typical leverage ratio was 25-to-1 [5], meaning that for every dollar of investor capital, LTCM borrowed approximately $25 to amplify its positions. In some instances, leverage reportedly reached 30-to-1 or even higher. This allowed the fund to magnify small arbitrage opportunities into significant profits. By 1998, LTCM had over $125 billion in assets under management, yet its capital base remained relatively small. The firm’s trading volume was staggering. At its peak, LTCM held positions totalling over $1 trillion in notional value across global markets, including government bonds, corporate debt, equities, and derivatives. This level of leverage meant that even a small move in asset prices could generate significant gains—or catastrophic losses.
Despite these risks, LTCM’s leadership exhibited immense confidence in its risk management models. On October 10, 1994, in its first shareholders’ report, LTCM presented a series of probability estimates for potential losses with misleading precision. According to these calculations, the probability of the fund losing 5% of its value in a typical year was estimated at 12%, while the likelihood of 10% or 15% losses was considered even lower. These figures reassured investors, fostering an illusion of control and stability [6].
The Fall of LTCM
However, in 1998, LTCM was struck by an unprecedented shock that exposed the fundamental flaws in its assumptions. The firm’s models, deeply rooted in statistical methods and equilibrium-based physics concepts, failed catastrophically in the face of extreme market conditions. The quants at LTCM had forgotten a crucial fact: unlike a controlled system in physics, financial markets are driven by human behaviour which LTCM’s models failed to adequately incorporate.
The firm’s downfall began in August 1998, when Russia unexpectedly defaulted on its government bonds, triggering a wave of global financial instability. LTCM had significant positions in Russian government debt and related assets that were assumed to converge in price. However, instead of converging, these spreads widened drastically, leading to massive losses on LTCM’s highly leveraged trades [7].
LTCM’s models had assumed that price movements followed a log-normal distribution, akin to how Brownian motion models random particle movement in physics. This assumption suggested that extreme events—so-called “black swan” events—were incredibly rare. However, financial markets do not adhere to the principles of ergodicity or stationary distributions as assumed by LTCM’s models. Instead, they experience sudden regime shifts, correlated panic behaviours, and liquidity crises that are not captured by standard physics-based models.
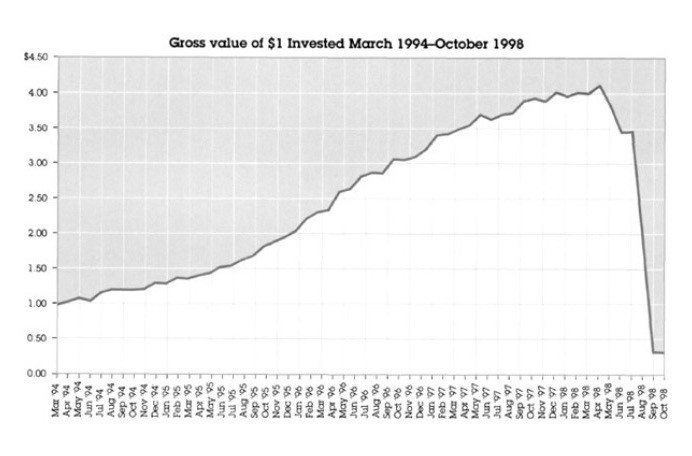
As the crisis unfolded, LTCM’s assumptions about market liquidity collapsed. The firm had expected to unwind its positions gradually, but the evaporation of liquidity made it impossible to exit trades without incurring catastrophic losses. By September 1998, LTCM had lost nearly 90% of its capital, with losses exceeding $4 billion in a matter of weeks. The fund’s collapse posed a systemic risk to the global financial system, as LTCM’s positions were deeply intertwined with major banks and institutions worldwide. With over $1 trillion in notional positions, LTCM’s failure threatened to trigger a broader financial crisis.
Recognizing the potential systemic catastrophe, the Federal Reserve Bank of New York intervened. They orchestrated a $3.6 billion bailout led by a consortium of major banks, including Goldman Sachs, Merrill Lynch, and J.P. Morgan. The goal was not to save LTCM itself, but to prevent a domino effect that could destabilize the entire global financial system.
LTCM’s collapse served as a stark warning about the dangers of excessive leverage and blind faith in quantitative models inspired by physics. The assumption that markets behave like closed, predictable systems was fatally flawed. Instead, financial markets are adaptive, dynamic, and subject to irrational herd behaviour, making them fundamentally different from physical systems governed by static laws. LTCM was ultimately liquidated in 2000, and its spectacular failure remains one of the most important lessons in the dangers of overreliance on physics-based financial models in an unpredictable world.