Section 4: Deriving the Black-Scholes Model

The initial assumptions of the model

Stock pays no dividends. This assumption simplifies the model because dividends would add an extra layer of complexity to the underlying asset’s price behaviour. It means we focus solely on the price changes of the asset, ignoring any cash flows from dividends [1].

There are no transaction costs or taxes. This simplifies the model by assuming that the costs of buying and selling the asset are negligible. These costs exist, but for simplicity, we ignore them in this model.

The market is efficient, and the risk-free (interest) rate is constant. Market efficiency means that all information is already reflected in asset prices. A constant risk-free rate allows us to treat the future value of money in a straightforward way, avoiding fluctuations in interest rates.

The option can be continuously rebalanced (no discrete rebalancing). In real life, you can’t adjust your portfolio in real-time without transaction costs or delays, but this assumption lets us simplify the modelling process by assuming continuous adjustments to the hedged portfolio.

The price of the underlying asset follows a geometric Brownian Motion:

$\frac{dS_{t}}{S_{t}} = \mu dt + \sigma d W_{t}$

Where:

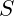$S$ is the price of the underlying asset.
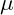$\mu$ is the drift (expected return) of the asset, the current interest rate.
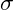$\sigma$ is the volatility of the asset.
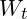$W_{t}$ is the Wiener process (stochastic term), basically the size of the Brownian motion movement in price.

Think of the asset price like a particle moving in a fluid: the drift term represents the average movement in a specific direction (like the particle’s average velocity), while the volatility is like the random collisions with molecules that cause the particle to move erratically.

Construct a Portfolio

$\Delta$ (often referred to as “the delta” in financial mathematics) shares of the stock. Delta has a positive or negative value depending on whether we are long or short on the stock respectively.
An option (European Call or Put). We use a call option in this derivation. 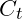$C_{t}$ is the premium or price of the option.

The goal is to make this portfolio risk-free by hedging against the stochastic movements of the underlying asset.

The value of the portfolio at time $t$ is:

$V_{t} = C_{t} - \Delta S_{t}$

The delta is preceded by a negative sign, as to hedge our call position, we must short the stock and hold a “negative” number of shares. This makes sense as if the stock loses value, then the call premium decreases. For the put case, if the stock increases in value, then the put premium decreases, therefore, to hedge our position we would long the stock.

Taking the differential:

$d V_{t} = d C_{t} - \Delta S_{t}$

Assuming the underlying stock follows geometric Brownian Motion (GBM):

$d S = \mu S d t - \sigma S d W_{t}$

Where the $dt$ term is the drift of the asset, and the $d W_{t}$ is the diffusion/Brownian Motion term. As the price of the option is a time-dependent function of a stochastic process, we use Ito’s Lemma to find the differential. It can be derived by Taylor expanding the function up to its second derivatives.

$d C_{t} = \frac {\partial C_{t}}{\partial t} dt + \frac {\partial C_{t}}{\partial S} dS + \frac{1}{2}(\frac{\partial^{2} C}{\partial S^{2}} d S^{2} + \frac{\partial^{2} C}{\partial t^{2}} d t^{2} )$

The first term is the change in the option’s value due to time.
The second term reflects how the option’s price changes with changes in the underlying asset price.
The third term comes from the volatility, accounting for the “spread” of the price due to randomness.

The $d t^{2}$ is very small, tending to zero so we ignore this term. This leaves:

$d V_{t} = \frac {\partial C_{t}}{\partial t} dt + \frac {\partial C_{t}}{\partial S} dS + \frac{1}{2}\frac{\partial^{2} C}{\partial S^{2}} d S^{2} - \Delta d S_{t}$

Equating “the delta” to $\frac{\partial C_{t}}{\partial S}$ (bear in mind, the delta is the number of shares held in the portfolio, and we are shorting the stock here due to the negative), the two $dS$ terms cancel. This creates a risk-free portfolio with respect to small movements in the stock price and is referred to as “delta hedged”. From GBM:

$dS^{2}_{t} = (\mu S_{t} dt + \sigma S_{t} d W_{t} )^{2}$

$d S^{2}_{t} = \mu ^{2} S^{2}_{t} d t^{2} + 2 \mu S^{2}_{t} dt d W_{t} + \sigma^{2} S^{2}_{t} d W^{2}_{t}$

$d S^{2}_{t} = \sigma^{2} S^{2}_{t} dt$

As $d W^{2}_{t}$ from Ito’s Calculus, and higher order differential terms disappear. Substituting this into the prior equation, proves zero dependence on $dS$ term, verifying this portfolio is “delta hedged”.

$dV_{t} = \frac{\partial C_{t}}{\partial t} dt + \frac{1}{2} \frac{\partial^{2} C}{\partial S^{2}} \sigma^{2} S^{2}_{t} dt$

Arbitrage free portfolio (bank account at interest rate, 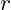$r$ )

The portfolio is risk-free if its change in value is deterministic (i.e. it does not depend on the stochastic term $d W_{t}$ ). There are no opportunities for riskless profits, and thus the model can provide a fair pricing formula for options [2]. If the portfolio is risk-free, its value should change just like a savings account that grows at the risk-free interest rate $r$ . This is a simplification that allows us to derive the Black-Scholes formula for pricing the option. There are therefore no opportunities for riskless profits, and thus the model can provide a fair pricing formula for options.

$dV_{t} = r V_{t} dt$

Where $V_{t} = C_{t} - \Delta S_{t}$ and thus:

$d V_{t} = r (C_{t} - \Delta S_{t}) dt$

Equating $dV_{t}$ and reminding ourselves of the fact $\Delta = \frac{\partial C}{\partial S}$ :

$r(C_{t} - \Delta S_{t}) dt = \frac{\partial C_{t}}{\partial t} dt + \frac{1}{2} \frac{\partial^{2} C}{\partial S^{2}} \sigma^{2} S^{2}_{t} dt$

$C_{t} = \frac{1}{r} \frac{\partial C_{t}}{t} + r S_{t} \frac{\partial C}{\partial S} + \frac{1}{2r} \frac{\partial^{2} C}{\partial S^{2}} \sigma^{2} S^{2}_{t}$

This is the renowned Black-Scholes option pricing model that pioneered a new generation of financial theory by providing a groundbreaking method for valuing options and enabled the most efficient risk management in financial markets at the time. However, the Black-Scholes model has many limitations due to the assumptions one makes in its derivation [3], and this proved to hurt Scholes and Merton later when their hedge fund, LTCM, failed catastrophically due to dramatic changes in the markets. These limitations and the case study will be discussed in more detail in sections 6 and 7 respectively.

References:

[1] Black, F. & Scholes, M., 1973. The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81(3), pp.637-654. Available at: https://doi.org/10.1086/260062

[2] Hull, J.C., 2017. Options, Futures, and Other Derivatives. 9th ed. Harlow: Pearson. ISBN: 978-0134446001.

[3] Heston, S., 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies, 6(2), pp.327–343. Available at: https://doi.org/10.1093/rfs/6.2.327