The Black-Scholes revolutionised the options market by providing a systematic approach to pricing European-style options. As noted above, before the development of the Black-Scholes model, options trading did not have an accepted, mathematically rigorous model for pricing an option. Instead, buyers and sellers had to haggle over prices resulting in an inefficient market [1].
Formalisation of Options Trading
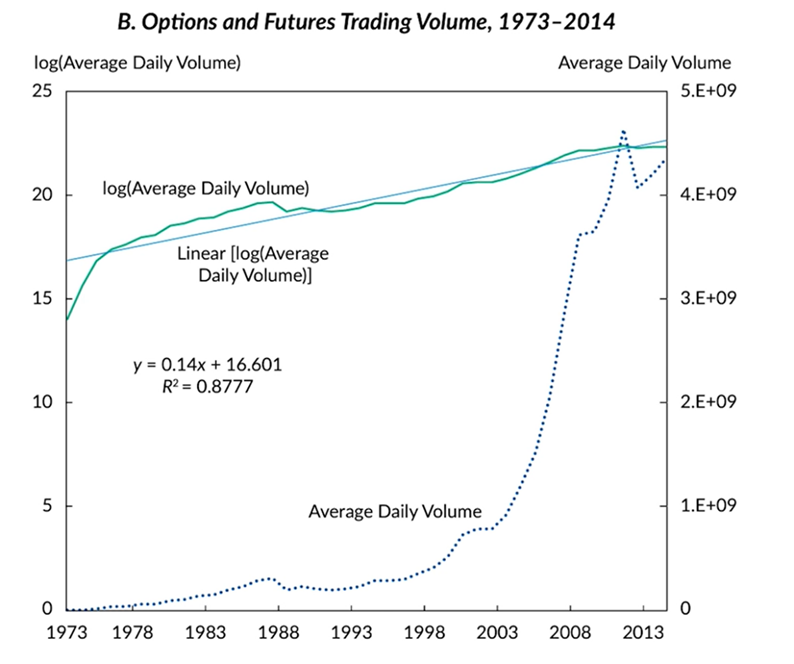
The initial and most significant application of the model was with the formation of formal option exchanges. The same year in which Black and Scholes published, the Chicago Board Options Exchange was founded with the mission to standardise options contracts using the Black-Scholes model. Within a few years, the Black-Scholes formula rapidly became the benchmark for trading options[2]. The model provided more consistent valuations which then attracted more investors as it removed a speculative aspect of options. This led to a rapid expansion in the options market with the volume of trades rising exponentially. Following the initial success of the model in options pricing, it rapidly became a substantial component of the strategies of major firms. Organisations like Goldman Sachs in the 80s and Morgan Stanley by the early 2000s integrated the model into their trading and risk management strategies.
Black – Scholes Applications in Delta Hedging
One application was in delta hedging, a strategy which involves maintaining a market-neutral stance which allowed institutions to have meticulous risk management, reducing loss from market fluctuations [4]. Essentially, it works in practice by using the Black-Scholes model to find delta, a measurement of how much the price of an option is expected to change in response to a $1 change in the underlying asset’s price. Let’s use an example to understand how the strategy is used.
Assume a trader holds a call option on 100 shares of a stock with a delta of 0.5 which means for every £1 increase in stock price, the options value increases by £0.50 per share. Initially, the stock increases in value and the trader can make a profit on the call option. Suddenly, the stock starts to drop which would reduce profits from the option. To hedge against this change, the trader sells 50 shares of the stock to remain in a delta-neutral position. Why 50?
The call option has a total delta of 0.5 x 100 shares = 50
By selling 50 shares (each with a delta of -1) the trader offsets the delta from the option.
Therefore, if the stock price fluctuates, the gains from the sold shares will offset the losses from the option and vice versa.
Expansion of the Black-Scholes Model
Though the model was heavily used for options pricing, there are other markets that have also grown as quickly. Some include the credit default swaps market, over-the-counter (OTC) derivatives market and securitized debt market. Many companies found use for the model in valuing employee stock options (ESOs), which are often included as part of compensation packages[5].
In today’s world, the Black-Scholes model remains a cornerstone of the world’s financial markets. Although there are many disadvantages to the model, traders use variations of the model that address the limitations. The framework brought forth by Fischer Black and Myron Scholes continues to shape the environment of financial markets, highlighting its enduring relevance in real-world applications.
